تقارن

تقارن

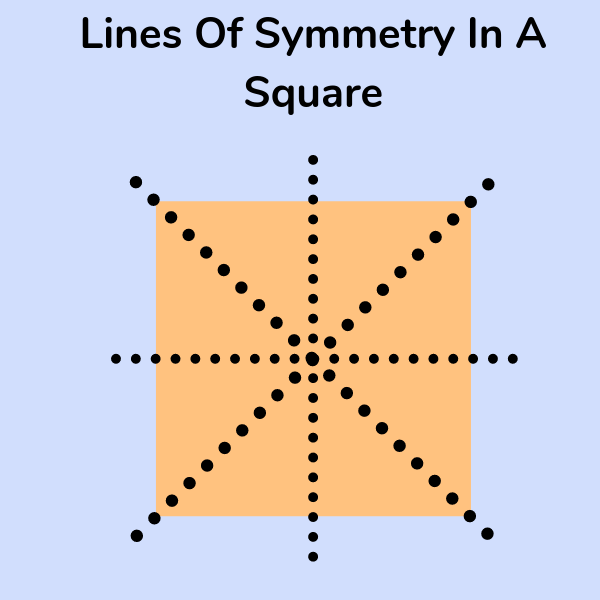
محور تقارن: محور تقارن در هر شکل، خطی است که اگر شکل را روی آن خط تا بزنیم، دو طرف آن شکل بر هم منطبق شوند.

رسم کردن قرینه ی هر شکل نسبت به یک خط را تقارن محوری میگویند.

عکس

مرکز تقارن: اگر نقطه ای مانند O در داخل یک چند ضلعی وجود داشته باشد به طوری که قرینه ی هر نقطه از آن شکل نسبت به نقطه ی O روی شکل واقع شود، می گوییم آن چند ضلعی دارای مرکز تقارن است. برای مثال در مربع و مستطیل محل برخورد خط های تقارن شکل است.

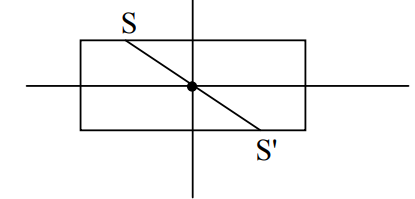
هر شکلی که دارای دو محور تقارن (خط تقارن) عمود بر هم باشد، نقطه تقاطع (برخورد) دو خط تقارن عمود بر هم آن مرکر تقارن شکل است. اما اگر شکلی دارای مرکز تقارن باشد نمی توان نتیجه گرفت که حتما آن شکل دارای دو خط تقارن عمود بر هم است.

در متوازی الاضلاع محل برخورد قطر های آن مرکز تقارن شکل است. در  صورتی که متوازی الاضلاع تقارن یا محور تقارن ندارد.

نکات

• هر n ضلعی منتظم n محور تقارن دارد.

• هر شکل را 360 درجه دوران دهیم بر خودش منطبق می شود.

• همه متوازی الاضلاع ها مرکز تقارن دارند.

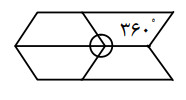
• در هر n ضلعی منتظم نقطه ای به نام o وجود دارد که از تمام گوشه های n ضلعی وصل کنیم، زاویه های مساوی ایجاد می شود که هر کدام از طریق   360 n محاسبه می شود.

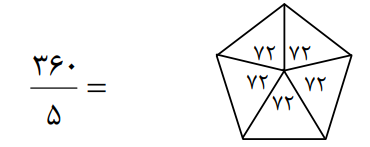
6 ضلعی منتظم در دوران های 60، 120، 180 و… مضارب 60 درجه حول o بر خودش منطبق می شود.

5 ضلعی منتظم بعد از دوران 72 درجه و مضارب آن حول o بر خودش منطبق می شود.

8 ضلعی منتظم بعد از دوران 45 درجه و مضارب آن حول o (مرکز) بر خودش منطبق می شود. پس هر n منتظم بعد از هر بار دوران 360n  بر خودش منطبق می شود.

برای هر n ضلعی محدب داریم:

1-  تعداد قطر n ضلعی منتظم

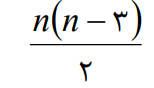
2- مجموع زوایای داخلی هر n ضلعی  180 × (2 – n)

3- مجموع زوایای خارجی هر n ضلعی =  360

4- اندازه یک زاویه داخلی n ضلعی منتظم

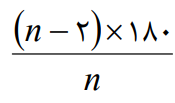
5- اندازه یک زاویه خارجی n ضلعی منتظم

  نکته: مجموع زوایای داخلی در مثلث 180 درجه می باشد.

کاشی کاری

در کاشی کاری، کاشی ها به گونه ای باید کنار هم قرار بگیرند که روی هم نباشند  در عین حال بین آنها فضای خالی هم نباشد.

پس شکل زیر می تواند یک کاشی کاری باشد

کاشی کاری مربعی

کاشی کاری ذوزنقه ای

ولی شکل رو به رو نمی تواند کاشی کاری باشد زیرا فضلی خالی بین کاشی ها بوجود آمده است.

توازی و تعامد

دو خط را موازی می گوییم هرگاه فاصله بین آن ها در تمامی نقاط به یک اندازه باشند به عبارت دیگر یکدیگر را قطع نکنند.

دو خط متقاطع: دو خطی را متقاطع می گوییم هرگاه یکدیگر را قطع کنند به عبارت دیگر موازی نباشند.

تذکر: در حالت متقاطع بودن اگر زاویه بین دو خط 90 درجه باشند خطوط را عمود بر هم می نامیم.

در حالت متقاطع بودن اگر دو خط روی یکدیگر قرار گیرند دو خط را منطبق می نامیم.

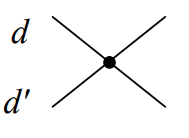
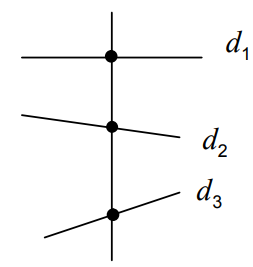
خط مورب: اگر خطی چند خط دیگر را در نقاط جدا از هم قطع کند، به آن خط مورب می گویند.

در شکل خط L در سه نقطه  جداگانه قطع کرده است. ( لازم نیست سه خط d1 , d2 , d3 موازی باشند)

اصول اقلیدوس

1- دو خط موازی با یک خط، باهم موازی اند.

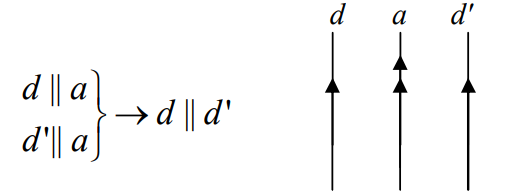
2- دو خط عمود بر یک خط با هم موازی اند.

3-  اگر خطی بر یکی از دو خط موازی عمود باشند بر دیگری نیز عمود است.

نکته : اگر خطی (خط مورب) دو خط موازی را قطع کند با آن دو خط 8 زاویه می سازد که چهار زاویه تند با هم چهار زاویه باز آن باهم مساوی اند و همچنین هر زاویه تند با هر زاویه بار مکمل است.