مختصات
مختصات
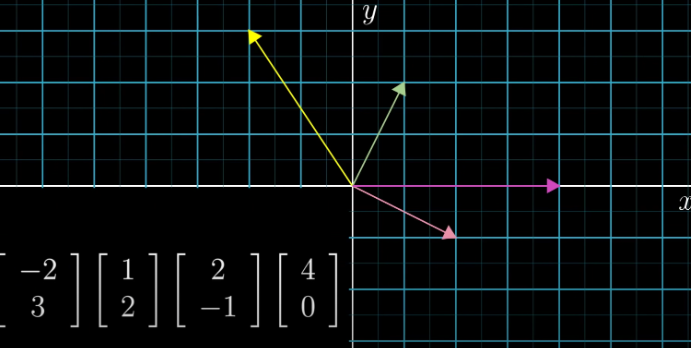
برای نمایش مختصات یک نقطه یا بردار در یک صفحه نیاز به دستگاهی به نام محور مختصات می باشند.
دستگاه مختصات از دو محور عمود بر هم تشکیل شده است. که محور افقی را محور طولها و محور عمودی را محور عرض ها می نامیم.
محل برخورد این دو محور را مبدا مختصات می نامیم. مبدا را با حرف o نمایش می دهیم. روی محور طول ها، از مبدا به سمت راست اعداد مثبت و از مبدا به سمت چپ اعداد منفی نوشته می شوند. روی محور عرض ها، از مبدا به بالا اعدا مثبت و به پایین اعداد منفی نوشته می شوند.
ناحیه های جدول مختصات
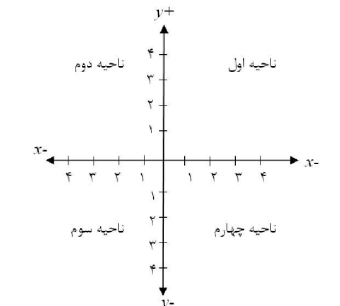
نکات
- مختصات هر نقطه در ناحیه اول به صورت (+x+ , y)
- مختصات هر نقطه در ناحیه دوم به صورت (-y+ , x )
- مختصات هر نقطه در ناحیه سوم به صورت ( -x- , y )
- مختصات هر نقطه در ناحیه چهارم به صورت ( +y- , x )
- اگر نقطه ای روی محور طول باشد عرض آن صفر است.
- اگر نقطه ای روی محور عرض باشد طول آن صفر است.
- اگر نقطه ای روی نیمساز ربع اول و سوم قرار داشته باشد مختصاتش به صورت (x=y) است.
- اگر نقطه ای روی نیمساز ربع دوم چهارم قرار داشته باشد مختصاتش به صورت ( x= -y ) است.
مختصات یک بردار
مقدار حرکت طولی و عرضی که از ابتدای بردار به سمت انتهای بردار انجام می شود مختصات بردار می گویند.
وقتی از ابتدای بردار به سمت انتهای بردار حرکت می کنیم اول یک حرکت طولی و سپس حرکت عرضی انجام می دهیم.
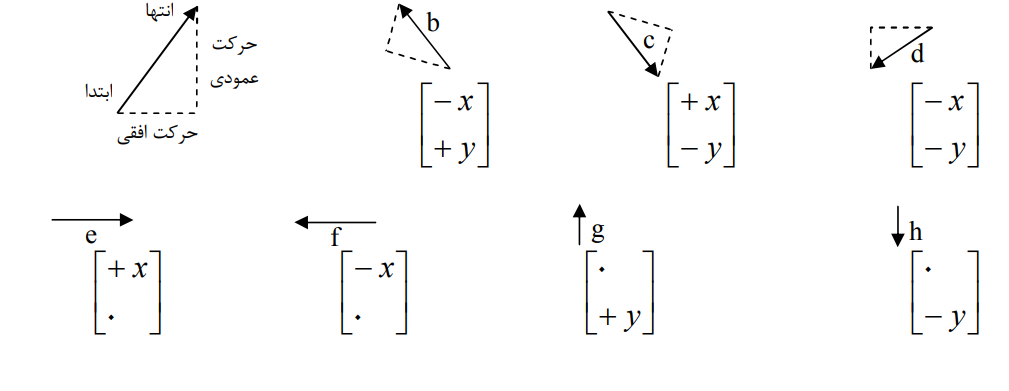
رسم بردار
برای رسم بردار طبق مراحل زیر عمل می کنیم.
1- نقطه ابتدای بردار را روی محور نشان می دهیم.
2- از این نقطه به اندازه طول بردار در جهت علامت آن، موازی محور طول ها حرکت می کنیم.
3- از ادامه حرکت به اندازه عرض بردار در جهت علامت آن، موازی محور عرض ها حرکت می کینم.
4- از ابتدا به انتهای حرکت وصل کرده و جهت را روی انتها قرار می دهیم.
جمع متناظر با یک بردار
مختصات ابتدای بردار + مختصات بردار = مختصات انتهای بردار
A + AB = B
( ابتدا A , طول AB , انتها B )
محاسبه ی حاصل جمع مختصات
برای محاسبه حاصل جمع چند مختصات کافی است طول ها را با هم و عرض ها را باهم جمع کنیم.
بردار انتقال
برداری است که هر نقطه (ابتدا) را به نقطه ی دیگری ( انتها) منتقل می کند. هر بردار یک انتقال می باشد.
نکته: نقطه ای از محور های مختصات به یک فاصله است به دلیل اینکه در فاصله منفی را در نظر نمیگیریم دو حالت ممکن است رخ دهد یا روی نیم ساز ربع اول و سوم است و با روی نیمساز دوم و چهارم.
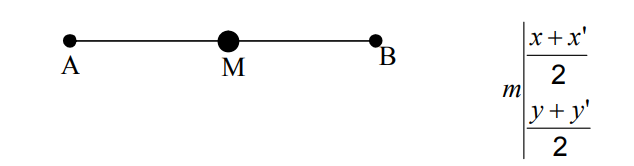
نکته: اگر مختصات دو سر پاره خط AB به صورت های x, y ) = a) و x’ , y’ ) = b ) باشند مختصات نقطه ی وسط پاره خط AB که آن را معمولا m می نامند به صورت زیر است:
نکته هایی درباره ی قرینه نقطه
- قرینه نقطه نسبت به محور عرض ها، عرض ثابت می ماند و فقط طول قرینه می شود.
- قرینه نقطه نسبت به محور طول ها، طول ثابت می ماند و فقط عرض قرینه می شود.
- قرینه نقطه نسبت به مبدا مختصات هم طول و هم عرض قرینه می شود.
- قرینه نقطه نسبت به نیم ساز ربع اول و سوم جای طول و عرض عوض می شود.
- قرینه نقطه نسبت به نیم ساز ربع دوم و چهارم هم جای طول و عرض عوض می شود و هم قرینه می شود.
مقدار AB همیشه مثبت است زیرا طول منفی وجود ندارد.

برای ارسال نظر لطفا ابتدا وارد حساب کاربری خود شوید. صفحه ورود و ثبت نام